Our funding comes from our readers, and we may earn a commission if you make a purchase through the links on our website.
Subnet Mask Cheat Sheet – A Tutorial and Thorough Guide to Subnetting!

UPDATED: August 28, 2023
Disclaimer: Even though the title of this article has “Cheat Sheet” in it, the best form of cheating is to thoroughly understand something first, and then apply shortcuts to your understanding. That is what we will be doing in this article.
In this article, we will be discussing subnetting, and focusing on useful techniques for subnetting. We will consider subnetting from a skill required on the job (e.g. as a network administrator) and also as a skill necessary for passing many exams, especially IOS & Cisco certification exams.
IP Addressing
We can’t talk about subnetting without first talking about IP addresses. Not to dwell too much on IP addressing, here is a quick and dirty guide to IPv4 addresses:
- An IP address uniquely identifies a device on a network
- An IPv4 address is made up of 32 bits
- To make IPv4 addresses easier to read, we use the dotted decimal notation i.e. the 32 bits are split into blocks of 8 (octets); each octet is converted to a decimal (between 0 and 255); and each block is separated by a decimal
- IPv4 addresses can be unicast (to-one), multicast (to-many), or broadcast (to-all)
- IPv4 addresses were originally designed to be classful – Class A to Class E
- Unicast IPv4 addresses can be split into two parts: Network portion and Host ID
- Class A (0-127) uses 8 bits for the network portion of the IP address, leaving 24 bits for host IDs
- Class B (128-191) uses 16 bits for the network portion of the IP address, leaving 16 bits for host IDs
- Class C (192-223) uses 24 bits for the network portion of the IP address, leaving 8 bits for host IDs
Let’s pause here for a bit because we are about touching on the defining moment of subnetting. So imagine in the older days, a device assigned the 20.12.1.21 IP address knew that this is a Class A address and therefore the network portion was 20.0.0.0 (first 8 bits) while the Host ID was 0.12.1.21 (last 24 bits). Similarly, a device with IP address 193.2.4.5 was able to identify 193.2.4.0 as the network while 0.0.0.5 is the host ID.
As the Internet grew, this method of IP addressing resulted in a lot of wastage. For example, an organization that needs only 2 IP addresses will get a Class C address block. With 8 bits for host IDs, a Class C address block gives 2^8 IP addresses i.e. 256 IP addresses.
Very Important: In reality, only 254 of these addresses are usable (for hosts) because the first address represents the network address while the last address represents the broadcast address of that network.
Subnetting
The classful nature of IP addressing was too rigid and resulted in wastage. In a bid to combat this, a technique called “subnetting” was implemented. By borrowing bits from the host portion of a network, smaller (sub) networks can be created within that network.
Let’s use an example to illustrate this. Imagine that an organization needs four IP address blocks for the different segments of its network and each segment of the network will have 50 hosts. Using classful IP addressing, the most conservative allocation will be 4 Class C address blocks. Let’s assume the organization gets the following blocks: 200.1.0.0, 200.1.1.0, 200.1.2.0, and 200.1.3.0.
As you can see, this allocation will result in a loss of (254 * 4) – (50 * 4) i.e. 816 IP addresses! Let’s take the 200.1.0.0 block as an example. In binary, this address will look like:

Since this is a Class C address, the first 24 bits (in red) will be used for the network portion while the last 8 bits (in green) will be used for host IDs.
Since we do not need all 8 bits for the hosts (we only need 50 host IPs), how about we borrow some bits from the host portion and use those bits to create “sub networks”? If we borrow 1 bit, our address block in binary becomes:

The 1 bit we borrowed is represented in purple. Remember that this is binary, meaning that this borrowed bit can either be 0 or 1. In effect, by borrowing one bit, we can create 2 subnets:
Borrowing 1 bit leaves us with 7 bits for the host IDs, meaning we can create (2^7 – 2) hosts IDs i.e. 126 host IDs. We subtract two to account for the network address (e.g. 200.1.0.0) and the broadcast address (e.g. 200.1.0.127).
If we borrow another bit from the host portion, we can create 4 subnets:
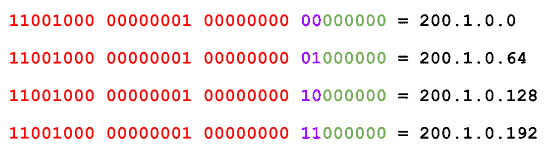
Now that we have borrowed 2 bits from the host portion, we are left with 6 bits for the host IDs. These 6 bits allow us to have (2^6 – 2) host IDs i.e. 62 host IDs. With this, we have met our requirement of 4 address blocks, each having space for (more than) 50 hosts. In this case, the wastage is (62 * 4) – (50 * 4) i.e. 48 IP addresses. Not too bad plus it allows for expansion.
Subnet Masks
If you look at it carefully, you will notice that we have now introduced another problem: how will devices know where the network portion stops and where the host portion begins? By default, a device using classful addressing will interpret 200.1.0.64, 200.1.0.128, and 200.1.0.192 as all being on the 200.1.0.0 network.
This clear this confusion, we use something called a subnet mask. A subnet mask is also 32 bits where the 1s represent the network portion and the 0s (or don’t care) represent the host portion.
For example, to represent the 200.1.0.64 subnet that we created, we will do the following:
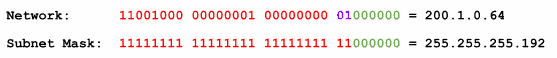
Therefore, the full representation for our 200.1.0.64 subnet is 200.1.0.64 255.255.255.192. The subnet mask can also be represented as a prefix length which is basically the number of bits that make up the network portion (i.e. counting the binary 1s). For example, 255.255.255.192 can also be represented as /26.
Subnetting Cheat Sheet
Now that we have gotten the basic understanding out of the way, let us look at common examples of how subnetting creeps up on you in real life and also in exams.
Number of Hosts in a Subnet
One thing you will need to do from time to time is figure out how many hosts you can have in a given subnet. For example, if you are designing a network, you need to know how many hosts the subnet you want to use can accommodate.
This is one of the easiest problems to solve. All you need to do is remember that the number of host bits in a subnet is 32 less the number of network bits. Also, you need to subtract 2 to get the usable IP addresses since the first IP address represents the network itself and the last IP address represents the broadcast address.
Therefore, the formula for calculating number of hosts is simply:
![]()
For example, in a /24 subnet, the number of hosts is:
![]()
Let’s take another example. How many usable IP addresses can we get from a /19 subnet?
![]()
What if you are given the subnet mask in dotted decimal notation? Even easier for /24 and greater. For example, how many usable IP addresses are there in 200.1.0.64 255.255.255.192? All you have to do is 256 – 192 – 2 i.e. 62.
Let’s try another one. How many usable IP addresses can you get in 192.168.10.0 255.255.255.248? Again, 256 – 248 – 2 = 6.
It gets tricky for subnet masks that are less than /24. For example, how many usable IP addresses are there in 172.16.23.0 255.255.240.0? For problems like this, it may be better to quickly convert the subnet mask to the prefix length format. So 255.255.240.0 is /20. Therefore, the number of usable IP addresses is 4094 i.e. 2^(32-20) – 2.
Minimum subnet size for a particular number of hosts
This type of question is somewhat related to the first but in the reverse form. For example, if you are designing a network that should accommodate 20 hosts, what is the minimum subnet size you can use?
To answer this, you need to determine how many host bits you will need to cover the number of hosts. That requires you to count in orders of 2:
- 1 bit: 2^1 = 2 possible IPs (including network/broadcast)
- 2 bits: 2^2 = 4 possible IPs
- 7 bits: 2^7 = 128 possible IPs
- 11 bits: 2^11 = 2048 possible IPs, etc.
Note: You will also need to factor in the 2 unusable IP addresses for network and broadcast addresses
So back to answer our initial question of the minimum subnet size to accommodate 20 hosts, the minimum number of host bits required is 5 bits (2^5 = 32). 4 bits (2^4 = 16) will be too small. So 5 bits used for the host IDs leaves us with 32 – 5 = 27 network bits. Therefore, the minimum subnet size we can use is /27.
Let’s try another one. What is the minimum subnet size we need to accommodate 127 hosts? If you are not careful, you will think the answer is 7 hosts bits meaning /25 subnet. However, a /25 subnet can accommodate 126 hosts because we need 2 IPs for the network and broadcast addresses. As such, a /24 subnet is the correct answer.
Number of Subnets in an Address Block
Finding the number of subnets in an address block is very easy as long as you know the reference address block! The formula is simply:
![]()
Let’s take examples. How many /27 subnets can you get from a /24 address block?
![]()
How about /25 subnets from a /17 block?
![]()
Wanting you to figure out the reference block is where some exams try to act smart. For example, how many /20 blocks can you get from the classful address block 171.44.0.0? In this scenario, they are also testing your knowledge of IP addresses classes. Looking at the 171.44.0.0 block, you will discover it is a Class B address and Class B uses 16 bits to represent the network portion. Therefore, number of subnets will be:
![]()
Note: Some questions around number of subnets used to be framed as follows: “How many subnets and hosts per subnet can you get from the network 172.25.0.0 255.255.255.192?” This makes no sense on its own because you can subnet a network however you want (e.g. /30, /29). However, from what we now know, this question is actually just asking you for the number of 255.255.255.192 (/26) subnets you can get from 172.25.0.0/16.
What subnet an address sits on
This kind of problems can be tricky especially when you see a weird looking address (as is always the case). The trick to answering this question is being able to determine the block size of the address block and counting up in that block size.
For example, on what subnet does the 156.67.154.75/28 IP address belong? The following steps will help us solve the problem:
- Determine how many network bits are in use. From this example, it is easy to see that 28 bits are used for the network portion.
- Determine the maximum number of bits in the boundary in which the subnet is. For example, /28 is in the fourth octet and the maximum number of bits from the first to fourth octet is 32 bits.
- Determine the subnet block size by subtracting the network bits from the answer in step 2 above, and raising to the power of 2. So in our example, 2^(32-28) = 16 subnet blocks.
- To find the subnet to which the address belongs, start at 0 (in whatever octet the subnet is) and increase by the block size. In this example, we know that a /28 subnet is somewhere in the fourth octet. Therefore, we go:
- 156.67.154.0/28
- 156.67.154.16/28
- 156.67.154.32/28
- 156.67.154.48/28
- 156.67.154.64/28
- 156.67.154.80/28
- 156.67.154.96/28, etc.
- Since .75 is greater than .64 and less than .80, the 156.67.154.75/28 address must belong in the 156.67.154.64/28 subnet.
It takes a bit of practice to get this. Let’s try another one. What subnet does the address 77.81.23.45/19 belong? Let’s run through it again quickly:
- Number of network bits = 19
- Subnet must sit in 3rd octet (since 19 is greater than 16 and less than 24). Therefore, maximum bits from 1st to 3rd octet is 24 bits.
- Block size = 2^(24-19) = 32
- Subnets starting from 0 in the 3rd octet are:
- 77.81.0.0/19
- 77.81.32.0/19
- 77.81.64.0/19, etc.
- Since .23 is greater than .0 and less than .32, then the 77.81.23.45/19 IP address belongs in the 77.81.0.0/19 subnet.
Let’s do one last one. What if you are given the subnet mask in dotted decimal notation, for example 10.135.45.67 255.224.0.0? This is even easier:
- We can skip counting the network bits. It is clear the subnet is in the 2nd octet so the block size will just be 256 – 224 = 32.
- Subnets starting from 0 in the 2nd octet are:
- 10.0.0.0 255.224.0.0
- 10.32.0.0 255.224.0.0
- 10.64.0.0 255.224.0.0
- 10.96.0.0 255.224.0.0
- 10.128.0.0 255.224.0.0
- 10.160.0.0 255.224.0.0, etc.
- Since .135 is greater than .128 and less than .160, then the subnet on which 10.135.45.67 255.224.0.0 belongs is 10.128.0.0 255.224.0.0 or 10.128.0.0/11.
Address Range in a Subnet
Another subnetting problem you may get is to determine the valid address range in a particular subnet. In some cases, the question will give you the subnet itself; in other cases, you will be given an address on the subnet. To solve this question, you must also determine the block size like in the previous section.
For example, what is the valid address range in the subnet 192.168.23.96/27? You can follow a similar method as in the previous section:
- Number of network bits = 27
- Subnet must sit in 4th octet. Maximum number of bits from 1st to 4th octet is 32.
- Subnet block size = 2^(32-27) = 32
- Subnets starting from 0 in octet 4:
- 192.168.23.0/27
- 192.168.23.32/27
- 192.168.23.64/27
- 192.168.23.96/27
- 192.168.23.128/27, etc.
- The valid address range is +1 IP address from the start of the network address to -2 IP addresses from the end of the subnet i.e. 192.168.23.97 to 192.168.23.126. The broadcast address is the last IP address in the subnet i.e. 192.168.23.127.
Let’s try another example. What is the network address, valid address range and broadcast address in the subnet to which the 172.25.65.123/18 address belongs?
- Number of network bits = 18
- Subnet must be in 3rd octet. Maximum number of bits from 1st to 3rd octet is 24.
- Subnet block size = 2^(24-18) = 64
- Subnets starting from 0 in octet 3:
- 172.25.0.0/18
- 172.25.64.0/18
- 172.25.128.0/18, etc.
- Therefore, 172.25.65.123/18 belongs in the 172.25.64.0/18 subnet and our answers are:
- Network address: 172.25.64.0/18
- Valid address range: 172.25.64.1 to 172.25.127.254
- Broadcast address: 172.25.127.255
Two Addresses on the same Subnet or Not?
The last type of question you can get is determining if two IP addresses are on the same subnet or not. Again, the trick to solving this problem is determining the subnet block size (of one of the addresses) and then calculating the valid host range to see if the 2nd address falls within the range.
Let’s try one example. Do the following addresses belong on the same subnet? 10.21.45.137/13 and 10.23.156.198/13? Let us pick the first address and determine the subnet and valid address range:
- Number of network bits = 13
- Subnet must be in 2nd octet. Maximum number of bits from 1st to 2nd octet is 16.
- Subnet block size = 2^(16-13) = 8
- Subnets starting from 0 in octet 2:
- 10.0.0.0/13
- 10.8.0.0/13
- 10.16.0.0/13
- 10.24.0.0/13, etc.
- Therefore 10.21.45.137 belongs on the 10.16.0.0/13 subnet which has valid address range of 10.16.0.1 to 10.23.255.254.
From our computation, 10.21.45.137/13 and 10.23.156.198/13 belong on the same subnet of 10.16.0.0/13.
Conclusion
Subnetting is Easy (or less difficult?) when you understand that IP addresses are in binary and you follow some simple rules like we have described in this article. As with anything, getting better at subnetting takes practice. You can find a useful subnetting practice site here.
Even though the world has moved away from classful networks to classless networks (and even CIDR), these subnetting rules are still valid for IPv4 addresses, especially from a design perspective.
While it is handy to have these subnetting skills at the tip of your head, you can also just use subnetting calculators like the one here. Its a Free Download and you can use it offline whenever you want!
Subnet Mask Cheat Sheet FAQs
How does a subnet mask work?
A subnet mask works by dividing the IP address into network and host portions based on the number of bits set to 1 in the mask.
Why is a subnet mask used?
A subnet mask is used to divide a large network into smaller subnets, allowing for better network organization and address utilization.
What is the difference between a subnet mask and an IP address?
An IP address is a numerical label assigned to each device connected to a computer network, while a subnet mask is used to divide the IP address into network and host portions.
How many subnet masks are there?
There are several subnet masks, including 255.255.255.0, 255.255.0.0, and 255.0.0.0, but the most common subnet mask used today is 255.255.255.0.
How do you calculate the number of subnets and hosts in a network?
You can calculate the number of subnets and hosts by counting the number of bits in the subnet mask and subtracting it from 32 (for IPv4) or 128 (for IPv6).
What is the default subnet mask for a Class C IP address?
The default subnet mask for a Class C IP address is 255.255.255.0.
Can a subnet mask be changed?
Yes, a subnet mask can be changed, but it requires reconfiguring the network devices and potentially renumbering the IP addresses in the subnet.

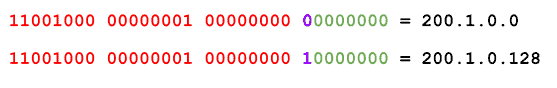


Free Subnet Calculator 100% FREE Calculator